Using GHCup!
When it comes to starting out with Haskell, I usually recommend installing Stack. Stack is an effective one-stop shop. It automatically installs Cabal for you, and it's also able to install the right version of GHC for your project. It installs GHC to a sandboxed location, so you can easily use different versions of GHC for different projects.
But there's another good program that can help with these needs! This program is called GHCup ("GHC up"). It fills a slightly different role from Stack, and it actually allows more flexibility in certain areas. Let's see how it works!
How do I install GHCup?
Just like Stack, you can install GHCup with a single terminal command. Per the documentation, you can use this command on Linux, Mac, and Windows Subsystem for Linux:
curl --proto '=https' --tlsv1.2 -sSf https://get-ghcup.haskell.org | shSee the link above for special instructions on a pure Windows setup.
What does GHCup do?
GHCup can handle the installation of all the important programs that make Haskell work. This includes, of course, the compiler GHC, Cabal, and Stack itself. What makes it special is that it can rapidly toggle between the different versions of all these programs, which can give you more flexibility.
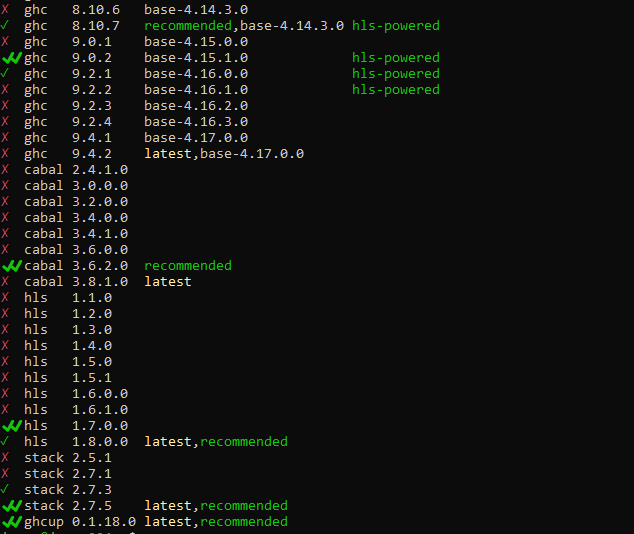
Once you install GHCup, this should install the recommended version of each of these. You can see what is installed with the command ghcup list.
The "currently installed" version of each has a double checkmark as you can see in the picture. When you use each of these commands with the --version argument, you should see the version indicated by GHCup:
>> stack --version
Version 2.7.5
>> cabal --version
cabal-install version 3.6.2.0
>> ghc --version
The Glorious Glasgow Haskell Compilation System, version 9.02How do I switch versions with GHCup?
Any entry with a single green checkmark is "installed" on your system but not "set". You can set it as the "global" version with the ghcup set command.
>> ghcup set ghc 8.10.7
[ Info ] GHC 8.10.7 successfully set as default version
>> ghc --version
The Glorious Glasgow Haskell Compilation System, version 8.10.7Versions with a red x aren't installed but are available to download. If a version isn't installed on your system, you can use ghcup install to get it:
>> ghcup install stack 2.7.1Then you need to set the version to use it:
>> ghcup set stack 2.7.1
>> stack --version
Version 2.7.1Note that the specific example with Stack might not work if you originally installed Stack through its own installer before using GHCup.
GHCup User Interface
On most platforms, you can also use the command: ghcup tui. This brings up a textual user interface that allows you to make these changes quickly! It will bring up a screen like this on your terminal, allowing you to use the arrow keys to set the versions as you desire.
All the commands are on screen, so it's very easy to use!
Notes on Stack and GHC
An important note on setting the "global" version of GHC is that this does not affect stack sandboxing. Even if you run ghcup set ghc 8.10.7, this won't cause any problems for a stack project using GHC 9.02. It will build as normal using 9.02.
So why does it even matter what the global version of GHC is? Let's find out!
GHCup and IDEs
Why do I mention GHCup when my last article was talking about IDEs? Well the one other utility you can install and customize with GHCup is the Haskell Language Server, which shows up in the GHCup output as the program hls. This is a special program that enables partial compilation, lint suggestions and library autocompletion within your IDE (among other useful features). As we'll explore in the next couple articles, Haskell Language Server can be a little tricky to use!
Even though Stack uses sandboxed GHC versions, HLS depends on the "global" version of GHC. And changing the "global" version to a particular version you've installed with stack is a little tricky if you aren't super familiar with Haskell's internals and also comfortable with the command line. So GHCup handles this smoothly.
Imagine we have two projects with different Stack resolvers (and in this case different GHC versions).
# stack.yaml #1
# (GHC 9.0.2)
resolver:
url: https://raw.githubusercontent.com/commercialhaskell/stackage-snapshots/master/lts/19.16
# stack.yaml #2
# (GHC 8.10.7)
resolver:
url: https://raw.githubusercontent.com/commercialhaskell/stackage-snapshots/master/lts/18.26If we want to get code suggestions in our first project, we just need to run this command before open it in the editor:
ghcup set ghc 9.0.2And if we then want to switch to our second project, we just need one command to get our hints again!
ghcup set ghc 8.10.7And of course, in addition to switching the GHC version, GHCup installs HLS for you and allows you to switch its version to keep up with updates.
Conclusion
With a basic understanding of HLS and switching GHC versions, we're now in a good position to start designing a really strong Haskell IDE! In the next couple of articles, we'll see a couple examples of this!
Keep up to date with all the latest news on Monday Morning Haskell by subscribing to our mailing list! This will also give you access to our subscriber resources!
What Makes a Good IDE?
Sometimes in the past I've read articles about people's IDE setups and thought "wow, they spend way too much time thinking about this." Now maybe sometimes people do go overboard. But on the other hand, I think it's fair to say I've been neglecting the importance of my development environment in my own practice.
A quick look at some of my videos in the last couple years can show you this fact. This whole playlist is a good example. I'm generally working directly with Vim with virtually no language features beyond syntax highlighting. I think my environment even lacked any semblance of auto-completion, so if I wasn't copying something directly, I would be writing the whole thing out.
If I wanted to compile or run my code, I would switch to a terminal opened in a separate window and manually enter commands. At the very least, I could switch between these terminals pretty easily. But opening new files and trying to compare files side-by-side was a big pain.
So after reflecting on these experiences, one of my resolutions this year has been to improve my Haskell development environment. In this first article on the subject, I'll consider the specific elements of what makes a good IDE and how we can use a systematic approach to build our ideal environment.
Listing Our Needs
Designing a good environment requires us to be intentional. This means thinking carefully about what we're using our environment for, and getting into the details of the specific actions we want.
So a good starting point is to list out the important actions we want to take within our editor. Here's my preliminary list:
- Open a file in a tab
- Switch between tabs
- Open files side-by-side (and switch between them)
- Open & close a navigation sidebar
- Use sidebar to open files
- Open up a terminal to run commands
- Switch between the terminal and file to edit
But having these features available is just the start. We also want to do things quickly!
Moving Fast
I used to play Starcraft for a few years. And while I wasn't that good, I was good enough to learn one important lesson to apply to programming. The keyboard is way more efficient than the mouse. The mouse gives the advantage of moving in 2D space. But overall the keyboard is much faster and more precise. So in your development environment, it's very important to learn to do as many things as possible with keyboard shortcuts.
So as a practical matter, I recommend thinking carefully about how you can accomplish your most common tasks (like the features we listed above) with the keyboard. Write these down if you have to!
It helps a lot if you use an editor that allows you to remap keyboard commands. This will give you much more control over how your system works and let you pick key-bindings that are more intuitive for you. Programs like Vim and Emacs allow extensive remapping and overall customization. However, More commercial IDEs like Visual Studio and IntelliJ will still usually allow you some degree of customization.
Speaking of Vim and Emacs, the general movement keys each has (for browsing through and editing your file) are extremely useful for helping improve your general programming speed. Most IDEs have plugins that allow you to incorporate these movement keys.
The faster you're able to move, the more programming will feel like an enjoyable experience, almost like a game! So you should really push yourself to learn these keyboard shortcuts instead of resorting to using the mouse, which might be more familiar at first. In a particular programming session, try to see how long you can go without using the mouse at all!
Language Features
The above features are useful no matter what language or platform you're using. Many of them could be described as "text editor" features, rather than features of a "development environment". But there are also specific things you'll want for the language you're working with.
Syntax highlighting is an essential feature, and autocomplete is extremely important. Basic autocomplete works with the files you have open, but more advanced autocomplete can also use suggestions from library functions.
At the next level of language features, we would want syntax hints, lint suggestions and partial compilation to suggest when we have errors (for compiled languages). These also provide major boosts to your productivity. You can correct errors on the fly, rather than trying to determine the right frequency to switch to your terminal, try compiling your code, and match up the errors with the relevant area of code.
One final area of improvement you could have is integrated build and test commands. Many commercial IDEs have these for particular language setups. But it can be a bit trickier to make these work for Haskell. This is why I still generally rely on opening a terminal instead of using such integrations.
Conclusion
In the next couple articles, I'll go through a few different options I've considered and experimented with for my Haskell development setup. I'll list a few pros and cons of each and give a few tips on starting out with them. I'll also go through a couple tools that are generally useful to making many development environments work with Haskell.
To make sure you're up to date on all our latest news, make sure you've subscribed to our mailing list! This will give you access to all our subscriber resources, including our Beginners Checklist!
Haskell for High Schoolers: Paradigm Conference!
Here's a quick announcement today, aimed at those younger Haskellers out there. If you're in middle school or high school (roughly age 18 and below), you should consider signing up for Paradigm Conference this coming weekend (September 23-25)! This is a virtual event aimed at teaching younger students about functional programming.
The first day of the conference consists of a Hackathon where you'll get the chance to work in teams to solve a series of programming problems. I've been emphasizing this sort of problem solving a lot in my streaming sessions, so I think it will be a great experience for attendees!
On the second day, there will be some additional coding activities, as well as workshops and talks from speakers, including yours truly. Since I'll be offline the whole weekend, my talk will be pre-recorded, but it will connect a lot of the work I've been doing in the last couple of months with respect to Data Structures and Dijkstra's algorithm. So if you've enjoyed those series independently, you might enjoy the connections I try to make between these ideas. This video talk will include a special offer for Haskell newcomers!
So to sign up and learn more, head over to the conference site, and start getting ready!
Everyday Applicatives!
I recently revised the Applicatives page on this site, and it got me wondering...when do I use applicatives in my code? Functors are simpler, and monads are more ubiquitous. But applicatives fill kind of an in-between role where I often don't think of them too much.
But a couple weeks ago I encountered one of those small coding problems in my day job that's easy enough to solve, but difficult to solve elegantly. And as someone who works with Haskell, of course I like to make my code as elegant as possible.
But since my day job is in C++, I couldn't find a good solution. I was thinking to myself the whole time, "there's definitely a better solution for this in Haskell". And it turns out I was right! And the answer in this case, was to functions specific to Applicative!
To learn more about applicative functors and other functional structures, make sure to read our Monads series! But for now, let's explore this problem!.
Setup
So at the most basic level, let's imagine we're dealing with a Messsage type that has a timestamp:
class Message {
Time timestamp;
...
}We'd like to compare two messages based on their timestamps, to see which one is closer to a third timestamp. But to start, our messages are wrapped in a StatusOr object for handling errors. (This is similar to Either in Haskell).
void function() {
...
Time baseTime = ...;
StatusOr<Message> message1 = ...;
StatusOr<Message> message2 = ...;
}I now needed to encode this logic:
- If only one message is valid, do some logic with that message
- If both messages are valid, pick the closer message to the
baseTimeand perform the logic. - If neither message is valid, do a separate branch of logic.
The C++ Solution
So to flesh things out more, I wrote a separate function signature:
void function() {
...
Time baseTime = ...;
StatusOr<Message> message1 = ...;
StatusOr<Message> message2 = ...;
optional<Message> closerMessage = findCloserMessage(baseTime, message1, message2);
if (closerMessage.has_value()) {
// Do logic with "closer" message
} else {
// Neither is valid
}
}
std::optional<Message> findCloserMessage(
Time baseTime,
const StatusOr<Message>& message1,
const StatusOr<Message>& message2) {
...
}So the question now is how to fill in this helper function. And it's simple enough if you embrace some branches:
std::optional<Message> findCloserMessage(
Time baseTime,
StatusOr<Message> message1,
StatusOr<Message> message2) {
if (message1.isOk()) {
if (message2.isOk()) {
if (abs(message1.value().timestamp - baseTime) < abs(message2.value().timestamp - baseTime)) {
return {message1.value()};
} else {
return {message2.value()};
}
} else {
return {message1.value()};
}
} else {
if (message2.isOk()) {
return {message2.value()};
} else {
return std::nullopt;
}
}
}Now technically I could combine conditions a bit in the "both valid" case and save myself a level of branching there. But aside from that nothing else really stood out to me for making this better. It feels like we're doing a lot of validity checks and unwrapping with .value()...more than we should really need.
The Haskell Solution
Now with Haskell, we can actually improve on this conceptually, because Haskell's functional structures give us better ways to deal with validity checks and unwrapping. So let's start with some basics.
data Message = Message
{ timestamp :: UTCTime
...
}
function :: IO ()
function = do
let (baseTime :: UTCTime) = ...
(message1 :: Either IOError Message) <- ...
(message2 :: EIther IOError Message) <- ...
let closerMessage' = findCloserMessage baseTime message1 message2
case closerMessage' of
Just closerMessage -> ...
Nothing -> ...
findCloserMessage ::
UTCTime -> Either IOError Message -> Either IOError Message -> Maybe Message
findCloserMessage baseTime message1 message2 = ...How should we go about implementing findCloserMessage?
The answer is in the applicative nature of Either! We can start by defining a function that operates directly on the messages and determines which one is closer to the base:
findCloserMessage baseTime message1 message2 = ...
where
f :: Message -> Message -> Message
f m1@(Message t1) m2@(Message t2) =
if abs (diffUTCTime t1 baseTime) < abs (diffUTCTime t2 basetime)
then m1 else m2We can now use the applicative operator <*> to apply this operation across our Either values. The result of this will be a new Either value.
findCloserMessage baseTime message1 message2 = ...
where
f :: Message -> Message -> Message
f m1@(Message t1) m2@(Message t2) =
if abs (diffUTCTime t1 baseTime) < abs (diffUTCTime t2 basetime)
then m1 else m2
bothValidResult :: Either IOError Message
bothValidResult = pure f <*> message1 <*> message2So if both are valid, this will be our result. But if either of our inputs has an error, we'll get this error as the result instead. What happens in this case?
Well now we can use the Alternative behavior of many applicative functors such as Either. This lets us use the <|> operator to combine Either values so that instead of getting the first error, we'll get the first success. So we'll combine our "closer" message if both are valid with the original messages:
import Control.Applicative
findCloserMessage baseTime message1 message2 = ...
where
f :: Message -> Message -> Message
f m1@(Message t1) m2@(Message t2) =
if abs (diffUTCTime t1 baseTime) < abs (diffUTCTime t2 basetime)
then m1 else m2
bothValidResult :: Either IOError Message
bothValidResult = pure f <*> message1 <*> message2
allResult :: Either IOError Message
allResult = bothValidResult <|> message1 <|> message2The last step is to turn this final result into a Maybe value:
import Control.Applicative
import Data.Either
findCloserMessage ::
UTCTime -> Either IOError Message -> Either IOError Message -> Maybe Message
findCloserMessage baseTime message1 message2 =
if isRight allResult then Just (fromRight allResult) else Nothing
where
f :: Message -> Message -> Message
f m1@(Message t1) m2@(Message t2) =
if abs (diffUTCTime t1 baseTime) < abs (diffUTCTime t2 basetime)
then m1 else m2
bothValidResult :: Either IOError Message
bothValidResult = pure f <*> message1 <*> message2
allResult :: Either IOError Message
allResult = bothValidResult <|> message1 <|> message2The vital parts of this are just the last 4 lines. We use applicative and alternative operators to simplify the logic that leads to all the validity checks and conditional branching in C++.
Conclusion
Is the Haskell approach better than the C++ approach? Up to you! It feels more elegant to me, but maybe isn't as intuitive for someone else to read. We have to remember that programming isn't a "write-only" activity! But these examples are still fairly straightforward, so I think the tradeoff would be worth it.
Now is it possible to do this sort of refactoring in C++? Possibly. I'm not deeply familiar with the library functions that are possible with StatusOr, but it certainly wouldn't be as idiomatic.
If you enjoyed this article, make sure to subscribe to our monthly newsletter! You should also check out our series on Monads and Functional Structures so you can learn more of these tricks!
My New Favorite Monad?
In my last article, I introduced a more complicated example of a problem using Dijkstra's algorithm and suggested MonadLogger as an approach to help debug some of the intricate helper functions.
But as I've started getting back to working on some of the "Advent of Code" type problems, I've come to the conclusion that this kind of logging might be more important than I initially realized. At the very least, it's gotten me thinking about improving my general problem solving process. Let's explore why.
Hitting a Wall
Here's an experience I've had quite a few times, especially with Haskell. I'll be solving a problem, working through the ideas in my head and writing out code that seems to fit. And by using Haskell, a lot of problems will be resolved just from making the types work out.
And then, ultimately, the solution is wrong. I don't get the answer I expected, even though everything seems correct.
So how do I fix this problem? A lot of times (unfortunately), I just look at the code, think about it some more, and eventually realize an idea I missed in one of my functions. This is what I would call an insight-based approach to debugging.
Insight is a useful thing. But used on its own, it's probably one of the worst ways to debug code. Why do I say this? Because insight is not systematic. You have no process or guarantee that you'll eventually come to the right solution.
So what are systematic approaches you can take?
Systematic Approaches to Debugging
Three general approaches come to my mind when I think about systematic debugging methods.
- Writing unit tests
- Using a debugging program (e.g. GDB)
- Using log statements
Unit Tests
The first approach is distinct from the other two in that it is a "black box" method. With unit tests, we provide a function with particular inputs and see if it produces the outputs we expect. We don't need to think about the specific implementation of the function in order to come up with these input/output pairs.
This approach has advantages. Most importantly, when we write unit tests, we will have an automated program that we can always run to verify that the function still behaves how we expect. So we can always refactor our function or try to improve its performance and still know that it's giving us the correct outputs.
Writing unit tests proactively (test driven development) can also force us to think about edge cases before we start programming, which will help us implement our function with these cases in mind.
However, unit testing has a few disadvantages as well. Sometimes it can be cumbersome to construct the inputs to unit-test intermediate functions. And sometimes it can be hard to develop non-trivial test cases that really exercise our code at scale, because we can't necessarily know the answer to harder cases beforehand. And sometimes, coming up with a unit test that will really find a good edge case takes the same kind of non-systematic insight that we were trying to avoid in the first place.
Unit tests can be tricky and time-consuming to do well, but for industry projects you should expect to unit test everything you can. So it's a good habit to get into.
Using a Debugger
The second approach on the list is more of a "white box" approach. Debuggers allow us to explore the interior state of our function while it is running and see if the values match our expectations.
So for example, the typical debugger can set a breakpoint so that the program pauses execution in the middle of our function. We can then explore all the values in scope at this point. And examining these values can tell us if the assumptions we're making about our code are correct. We can then step the program forward and see if these values update the way we expect.
However, it is a bit harder to use debugging programs with Haskell. With most imperative languages, the ordering of the machine code (at least when unoptimized) somewhat resembles the order of the code you write in the editor. But Haskell is not an imperative language, so the ordering of operations is more complicated. This is made even worse because of Haskell's laziness.
But debuggers are still worth pursuing! I'll be exploring this subject more in the future. For now, let's move on to our last approach.
Log Messages
What are the advantages of using a logging approach? Are "print statements" really the way to go?
Well this is the quickest and easiest way to get some information about your program. Anyone who's done a technical interview knows this. When something isn't going right in that kind of fast-paced situation, you don't have time to write unit tests. And attaching a debugger isn't an option in interview environments like coderpad. So throwing a quick print statement in your code can help you get "unstuck" without spending too much time.
But generally speaking, you don't want your program to be printing out random values. Once you've resolved your issue, you'll often get rid of the debugging statements. Since these statements won't become part of your production code, they won't remain as a way to help others understand and debug your code, as unit tests do.
Logging and Frustration in Haskell
Considering these three different methods, logging and print statements are the most common method for anyone who is first learning a language. Setting up a debugger can be a complex task that no beginner wants to go through. Nor does a novice typically want to spend the time to learn unit test frameworks just so they can solve basic problems.
This presents us with a conundrum in helping people to learn Haskell. Because logging is not intuitive in Haskell. Or rather, proper logging is not intuitive.
Showing someone the main :: IO () and then using functions like print and putStrLn is easy enough. But once beginners start writing "pure" functions to solve problems, they'll get confused about how to use logging statements, since the whole point of pure functions is that we can't just add print statements to them.
There are, of course, "unsafe" ways to do this with the trace library and unsafePerformIO. But even these options use patterns that are unintuitive for beginners to the language.
Start with Logger Monad
With these considerations, I'm going to start an experiment for a while. As I write solutions to puzzle problems (the current focus of my Haskell activity), I'm going to write all my code with a MonadLogger constraint. And I would consider the idea of recommending a beginner to do the same. My hypothesis is that I'll solve problems much more quickly with some systematic approach rather than unsystematic insight-driven-development. So I want to see how this will go.
Using MonadLogger is much more "pure" than using IO everywhere. While the most common instances of the logger monad will use IO, it still has major advantages over just using the IO monad from a "purity" standpoint. The logging can be disabled. You can also put different levels of logging into your program. So you can actually use logging statements to log a full trace of your program, but restrict it so that the most verbose statements are at DEBUG and INFO levels. In production, you would disable those messages so that you only see ERROR and WARN messages.
Most importantly, you can't do arbitrary IO activity with just a MonadLogger constraint. You can't open files or send network requests.
Of course, the price of this approach for a beginner is that the newcomer would have to get comfortable with having monadic code with a typeclass constraint before they necessarily understand these topics. But I'm not sure that's worse than using IO everywhere. And if it relieves the frustration of "I can't inspect my program", then I think it could be worthwhile for someone starting out with Haskell.
Conclusion
If you want to see me using this approach on real problems, then tune into my Twitch Stream! I usually stream 5 times a week for short periods. Some of these episodes will end up on my YouTube channel as well.
Meanwhile, you can also subscribe to the mailing list for more updates! This will give you access to Monday Morning Haskell's subscriber resources!
Dijkstra with Monads!
Last time on the blog, we considered this library version of Dijkstra's algorithm that you can find on Hackage.
dijkstra ::
(Foldable f, Num cost, Ord cost, Ord State)
=> (state -> f state) -- Function to generate list of neighbors
-> (state -> state -> cost) -- Function for cost generation
-> (state -> Bool) -- Destination predicate
-> state -- Initial state
-> Maybe (cost, [state]) -- Solution cost and path, Nothing if goal is unreachableHowever, there are a number of situations where this might be insufficient. In this article we'll consider some reasons why you would want to introduce monads into your solution for Dijkstra's algorithm. Let's explore some of these reasons!
Note! This is a "coding ideas" blog, rather than an "In Depth Tutorial" blog (see this article for a summary of different reading styles). Some of the code sampled are pretty well fleshed out, but some of them are more hypothetical ideas for you to try out on your own!
The Monadic Version
In addition to the "pure" version of Dijkstra's algorithm, the Algorithm.Search library also provides a "monadic" version. This version allows each of the input functions to act within a monad m, and of course gives its final result within this monad.
dijkstraM ::
(Monad m, Foldable f, Num cost, Ord cost, Ord State)
=> (state -> m (f state))
-> (state -> state ->m cost)
-> (state -> m Bool)
-> state
-> m (Maybe (cost, [state]))Now, if you've read our Monads Series, you'll know that a monad is a computational context. What are the kinds of contexts we might find ourselves in while performing Dijkstra's algorithm? Here are a few ideas to start with.
- We're reading our graph from a global state (mutable or immutable) 2.Our graph functions require reading a file or making a network call
- We would like to log the actions taken in our graph.
Let's go through some pseudocode examples to see how each of these could be useful.
Using a Global State
A global mutable state is represented with (of course) the State monad. An immutable global state uses the Reader monad to represent this context. Now, taken in a simple way, the Reader context could allow us to "pass the graph" without actually including it as an argument:
import qualified Data.Array as A
import Control.Monad.Reader
import Algorithm.Search (dijkstraM)
newtype Graph2D = Graph2D (A.Array (Int, Int) Int)
getNeighbors :: A.Array (Int, Int) Int -> (Int, Int) -> [(Int, Int)]
findShortestPath :: Graph2D -> (Int, Int) -> (Int, Int) -> Maybe (Int, [(Int, Int)])
findShortestPath graph start end = runReader
(dijkstraM neighbors cost (return . (== end)) start)
graph
where
cost :: (Int, Int) -> (Int, Int) -> Reader Graph2D Int
cost _ b = do
(Graph2D gr) <- ask
return $ gr A.! b
neighbors :: (Int, Int) -> Reader Graph2D [(Int, Int)]
neighbors source = do
(Graph2D gr) <- ask
return $ getNeighbors gr sourceIf we're already in this monad for whatever reason, then this could make sense. But on its own, it's not necessarily much of an improvement over partial function application.
A mutable state could be useful in certain circumstances as well. We likely wouldn't want to mutate the graph itself during iteration, as this would invalidate the algorithm. However, we could store certain metadata about what is happening during the search. For instance, we might want to track how often certain nodes are returned as a potential neighbor.
import qualified Data.HashMap.Strict as HM
import Control.Monad.State
import Data.Maybe (fromMaybe)
import Data.Foldable (find)
newtype Graph = Graph
{ edges :: HM.HashMap String [(String, Int)] }
type Metadata = HM.HashMap String Int
incrementKey :: String -> Metadata -> Metadata
incrementKey k metadata = HM.insert k (count + 1) metadata
where
count = fromMaybe 0 (HM.lookup k metadata)
findShortestPath :: Graph -> String -> String -> Maybe (Int, [String])
findShortestPath graph start end = evalState
(dijkstraM neighbors cost (return . (== end)) start)
HM.empty
where
cost :: String -> String -> State Metadata Int
cost n1 n2 =
let assocs = fromMaybe [] (HM.lookup n1 (edges graph))
costForN2 = find (\(n, _) -> n == n2) assocs
in case costForN2 of
Nothing -> return maxBound
Just (_, x) -> return x
neighbors :: String -> State Metadata [String]
neighbors node = do
let neighbors = fst <$> fromMaybe [] (HM.lookup node (edges graph))
metadata <- get
put $ foldr incrementKey metadata neighbors
return neighborsIn this implementation, we end up discarding our metadata, but if we wanted to we could include it as an additional output to help us understand what's happening in our search.
Reading from Files
In many cases, our "graph" is actually too big to fit within memory. In various cases, the entire graph could be distributed across many files on our system. Consider this simplified example:
data Location = Location
{ filename :: FilePath
, tag :: String
...
}Each file could track a certain "region" of your map, with references to certain locations "on the edge" whose primary data must be found in a different file. This means you'll need to have access to the file system to ensure you can find all the "neighbors" of a particular location: This means you'll need the IO monad in Haskell!
getMapNeighbors :: Location -> IO [Location]
-- Open original locations file
-- Find tag and include neighboring tags together with references to other filesThis matches the signature of the "neighbor generator" function in dijkstraM, so we'll be able to pass this function as the first argument.
Using Network Calls
Here's a fun example. Consider wiki-racing - finding the shortest path between the Wikipedia pages of two topics using only the links in the bodies of those pages. You could (theoretically) write a program to do this for you. You might create a type like this:
data WikiPage = WikiPage
{ pageTitle :: Text
, url :: URL
, bodyContentHtml :: Text
}In order to find the "neighbors" of this page, you would first have to parse the body HTML and find all the wikipedia links within it. This could be done in a pure fashion. But in order to create the WikiPage objects for each of those links, you would then need to send an HTML GET request to get their body HTML. Such a network call would require the IO monad (or some other MonadIO), so you're function will necessarily look like:
getWikiNeighbors :: WikiPage -> IO [Wikipage]But if you successfully implement that function, it's very easy to apply dijkstraM because the "cost" of each hop is always 1!
findShortestWikiPath :: Text -> Text -> IO (Maybe (Int, [WikiPage]))
findShortestWikiPath start end = do
firstPage <- findWikiPageFromTitle start
dijkstraM getWikiNeighbors (\_ _ -> return 1) (return . (== end)) firstPage
findWikiPageFromTitle :: Text -> IO WikiPage
...Of course, because the cost is always 1 this is actually a case where breadth first search would work more simply than Dijkstra's algorithm, so you could use the function bfsM from the same library!
Logging
Another common context for problem solving is the logging context. While we are solving our problem, we might want to record helpful statements telling us what is happening so that we can debug when things are going wrong. This happens using the MonadLogger typeclass, with a few interesting functions we can use, indicating different "levels" of logging.
class MonadLogger m where
...
logDebugN :: (MonadLogger m) => Text -> m ()
logInfoN :: (MonadLogger m) => Text -> m ()
logWarnN :: (MonadLogger m) => Text -> m ()
logErrorN :: (MonadLogger m) => Text -> m ()Now, unlike the previous two examples, this doesn't require the IO monad. A couple of the most common implementations of this monad class will, in fact, use IO functionality (printing to the screen or logging to a file). But this isn't necessary. You can still do logging in a "pure" way by storing the log messages in a sequence or other structure so you can examine them at the end of your program.
When would we want this for Dijkstra's algorithm? Well, sometimes the process of determining neighbors and costs can be complicated! I'll motivate this by introducing a more complicated example of a Dijkstra's algorithm problem.
A Complicated Example
Here's an example from last year's Advent of Code challenge. You can read the full description on that page. This problem demonstrates a less intuitive use of Dijkstra's algorithm.
The problem input is a "map" of sorts, showing a diagram of 4 rooms leading into one shared hallway.
#############
#...........#
###B#C#B#D###
#A#D#C#A#
#########Each of the four rooms is filled with "tokens", which come in 4 different varieties, A, B, C, D. (The Advent of Code description refers to them as "Amphipods", but that takes a while to write out, so I'm simplifying to "tokens").
We want to move the tokens around so that the A tokens end in the far left room, the B tokens in the room next to them, and so on.
#############
#...........#
###A#B#C#D###
#A#B#C#D#
#########But there are rules on how these tokens move. You can only move each token twice. Once to get it into an empty space in the hallway, and once to get it from the hallway to its final room. And tokens can't move "past" each other within the hallway.
Now each token has a specific cost for each space it moves.
A = 1 energy per move
B = 10 energy per move
C = 100 energy per move
D = 1000 energy per moveSo you want to move the token's into the final state with the lowest total cost.
Using Dijkstra's Algorithm
It turns out the most efficient solution (especially at a larger scale) is to treat this like a graph problem and use Dijkstra's algorithm! Each "state" of the problem is like a node in our graph, and we can move to certain "neighboring" nodes by moving tokens at a certain cost.
But the implementation turns out to be quite tricky! To give you an idea of this, here are some of the data type names and functions I came up with.
data Token = ...
data HallSpace = ...
data TokenGraphState = ...
tokenEdges :: TokenGraphState -> [(TokenGraphState, Int)]
updateStateWithMoveFromRoom :: Token -> HallSpace -> Int -> TokenGraphState -> (TokenGraphState, Int)
updateStateWithMoveFromHall :: Token -> HallSpace -> Int -> TokenGraphState -> (TokenGraphState, Int)
validMovesToHall :: Token -> TokenGraphState -> [(HallSpace, Int)]
validMoveToRoom :: TokenGraphState -> (HallSpace, TokenGraphState -> Maybe Token) -> Maybe (Int, Token, HallSpace)And these are just the functions with complex logic! There are even a few more simple helpers beyond this!
But when I ran this implementation, I didn't get the right answer! So how could I learn more about my solution and figure out what's going wrong? Unit testing and applying a formal debugger would be nice, but simply being able to print out what is going on in the problem is a quicker way to get started.
Haskell doesn't let you (safely) print from pure functions like I've written above, nor can you add values to a global logging state. So we can fix this by modifying the type signatures to instead use a MonadLogger constraint.
tokenEdges :: (MonadLogger m) => TokenGraphState -> m [(TokenGraphState, Int)]
updateStateWithMoveFromRoom :: (MonadLogger m) => Token -> HallSpace -> Int -> TokenGraphState -> (TokenGraphState, Int)
updateStateWithMoveFromHall :: (MonadLogger m) => Token -> HallSpace -> Int -> TokenGraphState -> m (TokenGraphState, Int)
validMovesToHall :: (MonadLogger m) => Token -> TokenGraphState -> m [(HallSpace, Int)]
validMoveToRoom :: (MonadLogger m) => TokenGraphState -> (HallSpace, TokenGraphState -> Maybe Token) -> m (Maybe (Int, Token, HallSpace))Now it's simple enough to modify a function to give us some important information about what's happening. Hopefully this is enough to help us solve the problem.
We would like to limit the number of functions that "need" the monadic action. But in practice, it is frustrating to find you need a monad in a deeper function of your algorithm because you'll need to modify everything on its call stack. So it might be a good idea to add at least a basic monad constraint from the beginner!
(Update: I did a full implementation of this particular problem that incorporates the logger monad!)
Conclusion
Next time on the blog, we'll start talking more generally about this idea of using monads to debug, especially MonadLogger. We'll consider the implementation pattern of "monads first" and different ways to approach this.
Make sure you're staying up to date with the latest news from Monday Morning Haskell by subscribing to our mailing list! This will also give you access to our subscriber resources!
Dijkstra Comparison: Looking at the Library Function
In the last few articles I've gone through my approach for generalizing Dijkstra's algorithm in Haskell. The previous parts of this included:
- Simple Form of Dijkstra's Algorithm
- Generalizing with a Multi-Param Typeclass
- Generalizing with a Type Family
- A 2D Graph example
But of course I wasn't the first person to think about coming up with a general form of Dijkstra's algorithm in Haskell. Today, we'll look at the API for a library implementation of this algorithm and compare it to the implementations I thought up.
Comparing Types
So let's look at the type signature for the library version of Dijkstra's algorithm.
dijkstra ::
(Foldable f, Num cost, Ord cost, Ord State)
=> (state -> f state) -- Function to generate list of neighbors
-> (state -> state -> cost) -- Function for cost generation
-> (state -> Bool) -- Destination predicate
-> state -- Initial state
-> Maybe (cost, [state]) -- Solution cost and path, Nothing if goal is unreachableWe'd like to compare this against the implementations in this series, but it's also useful to think about the second version of this function from the library: dijkstraAssoc. This version combines the functions for generating neighbors and costs:
dijkstraAssoc ::
(Num cost, Ord cost, Ord state)
=> (state -> [(state, cost)])
-> (state -> Bool)
-> state
-> Maybe (cost, [state])And now here's the signature for the Multi-Param typeclass version I wrote:
findShortestDistance ::
(Hashable node, Eq node, Num cost, Ord cost, DijkstraGraph graph)
=> graph -> node -> node -> Distance costWe can start the comparison by pointing out a few surface-level differences..
First, the library uses Nothing to represent a failure to reach the destination, instead of a Distance type with Infinity. This is a sensible choice to spare API users from incorporating an internal type into their own code. However, it does make some of the internal code more cumbersome.
Second, the library function also includes the full path in its result which is, of course, very helpful most of the time. The implementation details for this aren't too complicated, but it requires tracking an extra structure, so I have omitted it so far in this series.
Third, the library function takes a predicate for its goal, instead of relying on an equality. This helps a lot with situations where you might have many potential destinations.
Functional vs. Object Oriented Design
But the main structural difference between our functions is, of course, the complete lack of a "graph" type in the library implementation! Our version provides the graph object and adds a typeclass constraint so that we can get the neighboring edges. The library version just includes this function as a separate argument to the main function.
Without meaning to, I created an implementation that is more "object oriented". That is, it is oriented around the "object" of the graph. The library implementation is more "functional" in that it relies on passing important information as higher order functions, rather than associating the function specifically with the graph object.
Clearly the library implementation is more in keeping with Haskell's functional nature. Perhaps my mind gravitated towards an object oriented approach because my day job involves C++ and Python.
But the advantages of the functional approach are clear. It's much easier to generalize an algorithm in terms of functions, rather than with objects. By removing the object from the equation entirely, it's one less item that needs to have a parameterized (or templated) type in our final solution.
However, this only works well when functions are first class items that we can pass as input parameters. Languages like C++ and Java have been moving in the direction of making this easier, but the syntax is not nearly as clean as Haskell's.
Partial function application also makes this a lot easier. If we have a function that is written in terms of our graph type, we can still use this with the library function (see the examples below!). It is most convenient if the graph is our first argument, and then we can partially apply the function and get the right input for, say, dijkstraAssoc.
Applying The Library Function
To close this article, let's see these library functions in action with our two basic examples. Recall our original graph type:
import Data.HashMap.Strict (HashMap)
import qualified Data.HashMap.Strict as HM
data Distance a = Dist a | Infinity
deriving (Show, Eq)
newtype Graph = Graph
{ edges :: HashMap String [(String, Int)] }
graph1 :: Graph
graph1 = Graph $ HM.fromList
[ ("A", [("D", 100), ("B", 1), ("C", 20)])
, ("B", [("D", 50)])
, ("C", [("D", 20)])
, ("D", [])
]To fill in our findShortestDistance function, we can easily use dijkstraAssoc, using the edges field of our object to supply the assoc function.
import Algorithm.Search (dijkstraAssoc)
import Data.Maybe (fromMaybe)
findShortestDistance :: Graph -> String -> String -> Distance Int
findShortestDistance graph start end = case answer of
Just (dist, path) -> Dist dist
Nothing -> Infinity
where
costFunction node = fromMaybe [] (HM.lookup node (edges graph))
answer = dijkstraAssoc costFunction (== end) start
...
>> findShortestDistance graph1 "A" "D"
Distance 40But of course, we can also just skip our in-between function and use the full output of the library function. This is a little more cumbersome in our case, but it still works.
>> let costFunction node = fromMaybe [] (HM.lookup node (edges graph1))
>> dikjstraAssoc costFunction (== "D") "A"
Just (40, ["C", "D"]Notice that the library function omits the initial state when providing the final path.
Graph 2D Example
Now let's apply it to our 2D graph example as well. This time it's easier to use the original dijkstra function, rather than the version with "assoc" pairs.
import qualified Data.Array as A
newtype Graph2D = Graph2D (A.Array (Int, Int) Int)
getNeighbors :: A.Array (Int, Int) Int -> (Int, Int) -> [(Int, Int)]
getNeighbors input (row, col) = catMaybes [maybeUp, maybeDown, maybeLeft, maybeRight]
where
(maxRow, maxCol) = snd . A.bounds $ input
maybeUp = if row > 0 then Just (row - 1, col) else Nothing
maybeDown = if row < maxRow then Just (row + 1, col) else Nothing
maybeLeft = if col > 0 then Just (row, col - 1) else Nothing
maybeRight = if col < maxCol then Just (row, col + 1) else Nothing
graph2d :: Graph2D
graph2d = Graph2D $ A.listArray ((0, 0), (4, 4))
[ 0, 2, 1, 3, 2
, 1, 1, 8, 1, 4
, 1, 8, 8, 8, 1
, 1, 9, 9, 9, 1
, 1, 4, 1, 9, 1
]
findShortestPath2D :: Graph2D -> (Int, Int) -> (Int, Int) -> Maybe (Int, [(Int, Int)])
findShortestPath2D (Graph2D graph) start end = dijkstra
(getNeighbors graph)
(\_ b -> graph A.! b)
(== end)
start
...
>> findShortestDistance2D graph2d (0, 0) (4, 4)
Just (14, [(0, 1), (0, 2), (0, 3), (1, 3), (1, 4), (2, 4), (3, 4), (4, 4)]Conclusion
In the final part of this series we'll consider the "monadic" versions of these library functions and why someone would want to use them.
If you enjoyed this article, make sure to subscribe to our mailing list! This will keep you up to date on all the latest news about the site, as well as giving you access to our subscriber resources that will help you on your Haskell journey!
As always, you can find the full code implementation for this article on GitHub. But it is also given below in the appendix below.
Appendix - Full Code
module DijkstraLib where
import qualified Data.Array as A
import Data.HashMap.Strict (HashMap)
import qualified Data.HashMap.Strict as HM
import Data.Maybe (catMaybes, fromMaybe)
import Algorithm.Search (dijkstra, dijkstraAssoc)
data Distance a = Dist a | Infinity
deriving (Show)
newtype Graph = Graph
{ edges :: HashMap String [(String, Int)] }
graph1 :: Graph
graph1 = Graph $ HM.fromList
[ ("A", [("D", 100), ("B", 1), ("C", 20)])
, ("B", [("D", 50)])
, ("C", [("D", 20)])
, ("D", [])
]
findShortestDistance :: Graph -> String -> String -> Distance Int
findShortestDistance graph start end = case answer of
Just (dist, path) -> Dist dist
Nothing -> Infinity
where
costFunction node = fromMaybe [] (HM.lookup node (edges graph))
answer = dijkstraAssoc costFunction (== end) start
newtype Graph2D = Graph2D (A.Array (Int, Int) Int)
getNeighbors :: A.Array (Int, Int) Int -> (Int, Int) -> [(Int, Int)]
getNeighbors input (row, col) = catMaybes [maybeUp, maybeDown, maybeLeft, maybeRight]
where
(maxRow, maxCol) = snd . A.bounds $ input
maybeUp = if row > 0 then Just (row - 1, col) else Nothing
maybeDown = if row < maxRow then Just (row + 1, col) else Nothing
maybeLeft = if col > 0 then Just (row, col - 1) else Nothing
maybeRight = if col < maxCol then Just (row, col + 1) else Nothing
graph2d :: Graph2D
graph2d = Graph2D $ A.listArray ((0, 0), (4, 4))
[ 0, 2, 1, 3, 2
, 1, 1, 8, 1, 4
, 1, 8, 8, 8, 1
, 1, 9, 9, 9, 1
, 1, 4, 1, 9, 1
]
findShortestPath2D :: Graph2D -> (Int, Int) -> (Int, Int) -> Maybe (Int, [(Int, Int)])
findShortestPath2D (Graph2D graph) start end = dijkstra
(getNeighbors graph)
(\_ b -> graph A.! b)
(== end)
startDijkstra in a 2D Grid
We've now spent the last few articles looking at implementations of Dijkstra's algorithm in Haskell, with an emphasis on how to generalize the algorithm so it works for different graph types. Here's a quick summary in case you'd like to revisit some of this code, (since this article depends on these implementations).
Simple Implementation
Generalized with a Multi-param Typeclass
Generalized with a Type Family
Generalized Dijkstra Example
But now that we have a couple different examples of how we can generalize this algorithm, it's useful to actually see this generalization in action! Recall that our original implementation could only work with this narrowly defined Graph type:
newtype Graph = Graph
{ edges :: HashMap String [(String, Int)] }We could add type parameters to make this slightly more general, but the structure remains the same.
newtype Graph node cost = Graph
{ edges :: HashMap node [(node, cost)] }Suppose instead of this kind of explicit graph structure, we had a different kind of graph. Suppose we had a 2D grid of numbers to move through, and the "cost" of moving through each "node" was simply the value at that index in the grid. For example, we could have a grid like this:
[ [0, 2, 1, 3, 2]
, [1, 1, 8, 1, 4]
, [1, 8, 8, 8, 1]
, [1, 9, 9, 9, 1]
, [1, 4, 1, 9, 1]
]The lowest cost path through this grid uses the following cells, for a total cost of 14:
[ [0, 2, 1, 3, x]
, [x, x, x, 1, 4]
, [x, x, x, x, 1]
, [x, x, x, x, 1]
, [x, x, x, x, 1]
]We can make a "graph" type out of this grid in Haskell with a newtype wrapper over an Array. The index of our array will be a tuple of 2 integers, indicating row and column.
import qualified Data.Array as A
newtype Graph2D = Graph2D (A.Array (Int, Int) Int)For simplicity, we'll assume that our array starts at (0, 0).
Getting the "Edges"
Because we now have the notion of a DijkstraGraph, all we need to do for this type to make it eligible for our shortest path function is make an instance of the class. The tricky part of this is the function for dijkstraEdges.
We'll start with a more generic function to get the "neighbors" of a cell in a 2D grid. Most cells will have 4 neighbors. But cells along the edge will have 3, and those in the corner will only have 2. We start such a function by defining our type signature and the bounds of the array.
getNeighbors :: A.Array (Int, Int) Int -> (Int, Int) -> [(Int, Int)]
getNieghbors input (row, col) = ...
where
(maxRow, maxCol) = snd . A.bounds $ input
...Now we calculate the Maybe for a cell in each direction. We compare against the possible bounds in that direction and return Nothing if it's out of bounds.
getNeighbors :: A.Array (Int, Int) Int -> (Int, Int) -> [(Int, Int)]
getNeighbors input (row, col) = ...
where
(maxRow, maxCol) = snd . A.bounds $ input
maybeUp = if row > 0 then Just (row - 1, col) else Nothing
maybeDown = if row < maxRow then Just (row + 1, col) else Nothing
maybeLeft = if col > 0 then Just (row, col - 1) else Nothing
maybeRight = if col < maxCol then Just (row, col + 1) else NothingAnd as a last step, we use catMaybes to get all the "valid" neighbors.
getNeighbors :: A.Array (Int, Int) Int -> (Int, Int) -> [(Int, Int)]
getNeighbors input (row, col) = catMaybes [maybeUp, maybeDown, maybeLeft, maybeRight]
where
(maxRow, maxCol) = snd . A.bounds $ input
maybeUp = if row > 0 then Just (row - 1, col) else Nothing
maybeDown = if row < maxRow then Just (row + 1, col) else Nothing
maybeLeft = if col > 0 then Just (row, col - 1) else Nothing
maybeRight = if col < maxCol then Just (row, col + 1) else NothingWriting Class Instances
With this function, it becomes very easy to fill in our class instances! Let's start with the Multi-param class. We have to start by specifying the node type, and the cost type. As usual, our cost is a simple Int. But the node in this case is the index of our array - a tuple.
{-# LANGUAGE MultiParamTypeClasses #-}
{-# LANGUAGE FlexibleInstances #-}
instance DijkstraGraph Graph2D (Int, Int) Int where
...To complete the instance, we get our neighbors and combine them with the distance, which is calculated strictly from accessing the array at the index.
instance DijkstraGraph Graph2D (Int, Int) Int where
dijkstraEdges (Graph2D arr) cell = [(n, arr A.! n) | n <- neighbors]
where
neighbors = getNeighbors arr cellNow we can find the shortest distance! As before though, we have to be more explicit with certain types, as inference doesn't seem to work as well with these multi-param typeclasses.
dijkstraInput2D :: Graph2D
dijkstraInput2D = Graph2D $ A.listArray ((0, 0), (4, 4))
[ 0, 2, 1, 3, 2
, 1, 1, 8, 1, 4
, 1, 8, 8, 8, 1
, 1, 9, 9, 9, 1
, 1, 4, 1, 9, 1
]
-- Dist 14
cost2 :: Distance Int
cost2 = findShortestDistance dijkstraInput2D (0 :: Int, 0 :: Int) (4, 4)Type Family Instance
Filling in the type family version is essentially the same. All that's different is listing the node and cost types inside the definition instead of using separate parameters.
{-# LANGUAGE TypeFamilies #-}
instance DijkstraGraph Graph2D where
type DijkstraNode Graph2D = (Int, Int)
type DijkstraCost Graph2D = Int
dijkstraEdges (Graph2D arr) cell = [(n, arr A.! n) | n <- neighbors]
where
neighbors = getNeighbors arr cellAnd calling our shortest path function works here as well, this time without needing extra type specifications.
dijkstraInput2D :: Graph2D
dijkstraInput2D = Graph2D $ A.listArray ((0, 0), (4, 4))
[ 0, 2, 1, 3, 2
, 1, 1, 8, 1, 4
, 1, 8, 8, 8, 1
, 1, 9, 9, 9, 1
, 1, 4, 1, 9, 1
]
-- Dist 14
cost3 :: Distance Int
cost3 = findShortestDistance dijkstraInput2D (0, 0) (4, 4)Conclusion
Next time, we'll look at an even more complicated example for this problem. In the meantime, make sure you subscribe to our mailing list so you can stay up to date with the latest news!
As usual, the full code is in the appendix below. Note though that it depends on code from our previous parts: Dijkstra 2 (the Multi-param typeclass implementation) and Dijkstra 3, the version with a type family.
For the next part of this series, we'll compare this implementation with an existing library function!
Appendix
You can also find this code right here on GitHub.
{-# LANGUAGE MultiParamTypeClasses #-}
{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE TypeFamilies #-}
module Graph2D where
import qualified Data.Array as A
import Data.Maybe (catMaybes)
import qualified Dijkstra2 as D2
import qualified Dijkstra3 as D3
newtype Graph2D = Graph2D (A.Array (Int, Int) Int)
instance D2.DijkstraGraph Graph2D (Int, Int) Int where
dijkstraEdges (Graph2D arr) cell = [(n, arr A.! n) | n <- neighbors]
where
neighbors = getNeighbors arr cell
instance D3.DijkstraGraph Graph2D where
type DijkstraNode Graph2D = (Int, Int)
type DijkstraCost Graph2D = Int
dijkstraEdges (Graph2D arr) cell = [(n, arr A.! n) | n <- neighbors]
where
neighbors = getNeighbors arr cell
getNeighbors :: A.Array (Int, Int) Int -> (Int, Int) -> [(Int, Int)]
getNeighbors input (row, col) = catMaybes [maybeUp, maybeDown, maybeLeft, maybeRight]
where
(maxRow, maxCol) = snd . A.bounds $ input
maybeUp = if row > 0 then Just (row - 1, col) else Nothing
maybeDown = if row < maxRow then Just (row + 1, col) else Nothing
maybeLeft = if col > 0 then Just (row, col - 1) else Nothing
maybeRight = if col < maxCol then Just (row, col + 1) else Nothing
dijkstraInput2D :: Graph2D
dijkstraInput2D = Graph2D $ A.listArray ((0, 0), (4, 4))
[ 0, 2, 1, 3, 2
, 1, 1, 8, 1, 4
, 1, 8, 8, 8, 1
, 1, 9, 9, 9, 1
, 1, 4, 1, 9, 1
]
cost2 :: D2.Distance Int
cost2 = D2.findShortestDistance dijkstraInput2D (0 :: Int, 0 :: Int) (4, 4)
cost3 :: D3.Distance Int
cost3 = D3.findShortestDistance dijkstraInput2D (0, 0) (4, 4)Dijkstra with Type Families
In the previous part of this series, I wrote about a more general form of Dijkstra’s Algorithm in Haskell. This implementation used a Multi-param Typeclass to encapsulate the behavior of a “graph” type in terms of its node type and the cost/distance type. This is a perfectly valid implementation, but I wanted to go one step further and try out a different approach to generalization.
Type Holes
In effect, I view this algorithm as having three “type holes”. In order to create a generalized algorithm, we want to allow the user to specify their own “graph” type. But we need to be able to refer to two related types (the node and the cost) in order to make our algorithm work. So we can regard each of these as a “hole” in our algorithm.
The multi-param typeclass fills all three of these holes at the “top level” of the instance definition.
class DijkstraGraph graph node cost where
...But there’s a different way to approach this pattern of “one general class and two related types”. This is to use a type family.
Type Families
A type family is an extension of a typeclass. While a typeclass allows you to specify functions and expressions related to the “target” type of the class, a type family allows you to associate other types with the target type. We start our definition the same way we would with a normal typeclass, except we’ll need a special compiler extension:
{-# LANGUAGE TypeFamilies #-}
class DijkstraGraph graph where
...So we’re only specifying graph as the “target type” of this class. We can then specify names for different types associated with this class using the type keyword.
class DijkstraGraph graph where
type DijkstraNode graph :: *
type DijkstraCost graph :: *
...For each type, instead of specifying a type signature after the colons (::), we specify the kind of that type. We just want base-level types for these, so they are *. (As a different example, a monad type like IO would have the kind * -> * because it takes a type parameter).
Once we’ve specified these type names, we can then use them within type signatures for functions in the class. So the last piece we need is the edges function, which we can write in terms of our types.
class DijkstraGraph graph where
type DijkstraNode graph :: *
type DijkstraCost graph :: *
dijkstraEdges :: graph -> DijkstraNode graph -> [(DijkstraNode graph, DijkstraCost graph)]Making an Instance of the Type Family
It’s not hard now to make an instance for this class, using our existing Graph String Int concept. We again use the type keyword to specify that we are filling in the type holes, and define the edges function as we have before:
{-# LANGUAGE FlexibleInstances #-}
instance DijkstraGraph (Graph String Int) where
type DijkstraNode (Graph String Int) = String
type DijkstraCost (Graph String Int) = Int
dijkstraEdges graph node = fromMaybe [] (HM.lookup node (edges graph))This hasn’t fixed the “re-statement of parameters” issue I mentioned last time. In fact we now restate them twice. But with a more general type, we wouldn’t necessarily have to parameterize our Graph type anymore.
Updating the Type Signature
The last thing to do now is update the type signatures within our function. Instead of using separate graph, node, and cost parameters, we’ll just use one parameter g for the graph, and define everything in terms of g, DijkstraNode g, and DijkstraCost g.
First, let’s remind ourselves what this looked like for the multi-param typeclass version:
findShortestDistance ::
forall graph node cost. (Hashable node, Eq node, Num cost, Ord cost, DijkstraGraph graph node cost) =>
graph -> node -> node -> Distance costAnd now with the type family version:
findShortestDistance ::
forall g. (Hashable (DijkstraNode g), Eq (DijkstraNode g), Num (DijkstraCost g), Ord (DijkstraCost g), DijkstraGraph g) =>
g -> DijkstraNode g -> DijkstraNode g -> Distance (DijkstraCost g)The “simpler” typeclass ends up being shorter. But the type family version actually has fewer type arguments (just g instead of graph, node, and cost). It’s up to you which you prefer.
And don’t forget, type signatures within the function will also need to change:
processQueue ::
DijkstraState (DijkstraNode g) (DijkstraCost g) ->
HashMap (DijkstraNode g) (Distance (DijkstraCost g))Aside from that, the rest of this function works!
graph1 :: Graph String Int
graph1 = Graph $ HM.fromList
[ ("A", [("D", 100), ("B", 1), ("C", 20)])
, ("B", [("D", 50)])
, ("C", [("D", 20)])
, ("D", [])
]
...
>> findShortestDistance graph1 “A” “D”
Dist 40Unlike the multi-param typeclass version, this one has no need of specifying the final result type in the expression. Type inference seems to work better here.
Conclusion
Is this version better than the multi-param typeclass version? Maybe, maybe not, depending on your taste. It has some definite weaknesses in that type families are more of a foreign concept to more Haskellers, and they require more language extensions. The type signatures are also a bit more cumbersome. But, in my opinion, the semantics are more correct by making the graph type the primary target and the node and cost types as simply “associated” types.
In the next part of this series, we’ll apply these different approaches to some different graph types. This will demonstrate that the approach is truly general and can be used for many different problems!
Below you can find the full code, or you can follow this link to see everything on GitHub!
Appendix - Full Code
{-# LANGUAGE FlexibleContexts #-}
{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE TypeFamilies #-}
{-# LANGUAGE ScopedTypeVariables #-}
module Dijkstra3 where
import Data.Hashable (Hashable)
import qualified Data.Heap as H
import Data.Heap (MinPrioHeap)
import qualified Data.HashSet as HS
import Data.HashSet (HashSet)
import Data.HashMap.Strict (HashMap)
import qualified Data.HashMap.Strict as HM
import Data.Maybe (fromMaybe)
data Distance a = Dist a | Infinity
deriving (Show, Eq)
instance (Ord a) => Ord (Distance a) where
Infinity <= Infinity = True
Infinity <= Dist x = False
Dist x <= Infinity = True
Dist x <= Dist y = x <= y
addDist :: (Num a) => Distance a -> Distance a -> Distance a
addDist (Dist x) (Dist y) = Dist (x + y)
addDist _ _ = Infinity
(!??) :: (Hashable k, Eq k) => HashMap k (Distance d) -> k -> Distance d
(!??) distanceMap key = fromMaybe Infinity (HM.lookup key distanceMap)
newtype Graph node cost = Graph
{ edges :: HashMap node [(node, cost)] }
class DijkstraGraph graph where
type DijkstraNode graph :: *
type DijkstraCost graph :: *
dijkstraEdges :: graph -> DijkstraNode graph -> [(DijkstraNode graph, DijkstraCost graph)]
instance DijkstraGraph (Graph String Int) where
type DijkstraNode (Graph String Int) = String
type DijkstraCost (Graph String Int) = Int
dijkstraEdges graph node = fromMaybe [] (HM.lookup node (edges graph))
data DijkstraState node cost = DijkstraState
{ visitedSet :: HashSet node
, distanceMap :: HashMap node (Distance cost)
, nodeQueue :: MinPrioHeap (Distance cost) node
}
findShortestDistance :: forall g. (Hashable (DijkstraNode g), Eq (DijkstraNode g), Num (DijkstraCost g), Ord (DijkstraCost g), DijkstraGraph g) => g -> DijkstraNode g -> DijkstraNode g -> Distance (DijkstraCost g)
findShortestDistance graph src dest = processQueue initialState !?? dest
where
initialVisited = HS.empty
initialDistances = HM.singleton src (Dist 0)
initialQueue = H.fromList [(Dist 0, src)]
initialState = DijkstraState initialVisited initialDistances initialQueue
processQueue :: DijkstraState (DijkstraNode g) (DijkstraCost g) -> HashMap (DijkstraNode g) (Distance (DijkstraCost g))
processQueue ds@(DijkstraState v0 d0 q0) = case H.view q0 of
Nothing -> d0
Just ((minDist, node), q1) -> if node == dest then d0
else if HS.member node v0 then processQueue (ds {nodeQueue = q1})
else
-- Update the visited set
let v1 = HS.insert node v0
-- Get all unvisited neighbors of our current node
allNeighbors = dijkstraEdges graph node
unvisitedNeighbors = filter (\(n, _) -> not (HS.member n v1)) allNeighbors
-- Fold each neighbor and recursively process the queue
in processQueue $ foldl (foldNeighbor node) (DijkstraState v1 d0 q1) unvisitedNeighbors
foldNeighbor current ds@(DijkstraState v1 d0 q1) (neighborNode, cost) =
let altDistance = addDist (d0 !?? current) (Dist cost)
in if altDistance < d0 !?? neighborNode
then DijkstraState v1 (HM.insert neighborNode altDistance d0) (H.insert (altDistance, neighborNode) q1)
else ds
graph1 :: Graph String Int
graph1 = Graph $ HM.fromList
[ ("A", [("D", 100), ("B", 1), ("C", 20)])
, ("B", [("D", 50)])
, ("C", [("D", 20)])
, ("D", [])
]Generalizing Dijkstra's Algorithm
Earlier this week, I wrote a simplified implementation of Dijkstra’s algorithm. You can read the article for details or just look at the full code implementation here on GitHub. This implementation is fine to use within a particular project for a particular purpose, but it doesn’t generalize very well. Today we’ll explore how to make this idea more general.
I chose to do this without looking at any existing implementations of Dijkstra’s algorithm in Haskell libraries to see how my approach would be different. So at the end of this series I’ll also spend some time comparing my approach to some other ideas that exist in the Haskell world.
Parameterizing the Graph Type
So why doesn’t this approach generalize? Well, for the obvious reason that my module defines a specific type for the graph:
data Graph = Graph
{ graphEdges :: HashMap String [(String, Int)] }So, for someone else to re-use this code from the perspective of a different project, they would have to take whatever graph information they had, and turn it into this specific type. And their data might not map very well into String values for the nodes, and they might also have a different cost type in mind than the simple Int value, with Double being the most obvious example.
So we could parameterize the graph type and allow more customization of the underlying values.
data Graph node cost = Graph
{ graphEdges :: HashMap node [(node, cost)] }The function signature would have to change to reflect this, and we would have to impose some additional constraints on these types:
findShortestDistance :: (Hashable node, Eq node, Num cost, Ord cost) =>
Graph node cost -> node -> node -> Distance costGraph Enumeration
But this would still leave us with an important problem. Sometimes you don’t want to have to enumerate the whole graph. As is, the expression you submit as the "graph" to the function must have every edge enumerated, or it won’t give you the right answer. But many times, you won’t want to list every edge because they are so numerous. Rather, you want to be able to list every edge simply from a particular node. For example:
edgesForNode :: Graph node cost -> node -> [(node, cost)]How can we capture this behavior more generally in Haskell?
Using a Typeclass
Well one of the tools we typically turn to for this task is a typeclass. We might want to define something like this:
class DijkstraGraph graph where
dijkstraEdges :: graph node cost -> node -> [(node, cost)]However, it quickly gets a bit strange to try to do this with a simple typeclass because of the node and cost parameters. It’s difficult to resolve the constraints we end up needing because these parameters aren’t really part of our class.
Using a Multi-Param Typeclass
We could instead try having a multi-param typeclass like this:
{-# LANGUAGE MultiParamTypeClasses #-}
class DijkstraGraph graph node cost where
dijkstraEdges :: graph -> node -> [(node, cost)]This actually works more smoothly than the previous try. We can construct an instance (if we allow flexible instances).
{-# LANGUAGE FlexibleInstances #-}
import qualified Data.HashMap as HM
import Data.Maybe (fromMaybe)
instance DijkstraGraph (Graph String Int) String Int where
dijkstraEdges g n = fromMaybe [] (HM.lookup n (edges g))And we can actually use this class in our function now! It mainly requires changing around a few of our type signatures. We can start with our DijkstraState type, which must now be parameterized by the node and cost:
data DijkstraState node cost = DijkstraState
{ visitedSet :: HashSet node
, distanceMap :: HashMap node (Distance cost)
, nodeQueue :: MinPrioHeap (Distance cost) node
}And, of course, we would also like to generalize the type signature of our findShortestDistance function. In its simplest form, we would like use this:
findShortestDistance :: graph -> node -> node -> Distance costHowever, a couple extra items are necessary to make this work. First, as above, our function is the correct place to assign constraints to the node and cost types. The node type must fit into our hashing structures, so it should fulfill Eq and Hashable. The cost type must be Ord and Num in order for us to perform our addition operations and use it for the heap. And last of course, we have to add the constraint regarding the DijkstraGraph itself:
findShortestDistance ::
(Hashable node, Eq node, Num cost, Ord cost, DijkstraGraph graph) =>
graph -> node -> node -> Distance costNow, if we want to use the graph, node, and cost types within the “inner” type signatures of our function, we need one more thing. We need a forall specifier on the function so that the compiler knows we are referring to the same types.
{-# LANGUAGE ScopedTypeVariables #-}
findShortestDistance :: forall graph node cost.
(Hashable node, Eq node, Num cost, Ord cost, DijkstraGraph graph) =>
graph -> node -> node -> Distance costWe can now make one change to our function so that it works with our class.
processQueue :: DijkstraState node cost -> HashMap node (Distance cost)
processQueue = ...
-- Previously
-- allNeighbors = fromMaybe [] (HM.lookup node (edges graph))
-- Updated
allNeighbors = dijkstraEdges graph nodeAnd now we’re done! We can again, verify the behavior. However, we do run into some difficulties in that we need some extra type specifiers to help the compiler figure everything out.
graph1 :: Graph String Int
graph1 = Graph $ HM.fromList
[ ("A", [("D", 100), ("B", 1), ("C", 20)])
, ("B", [("D", 50)])
, ("C", [("D", 20)])
, ("D", [])
]
...
>> :set -XFlexibleContexts
>> findShortestDistance graph1 :: Distance Int
Dist 40Conclusion
Below in the appendix is the full code for this part. You can also take a look at it on Github here.
For various reasons, I don’t love this attempt at generalizing. I especially don't like the "re-statement" of the parameter types in the instance. The parameters are part of the Graph type and are separately parameters of the class. This is what leads to the necessity of specifying the Distance Int type in the GHCI session above. We could avoid this if we don't parameterize our Graph type, which is definitely an option.
In the next part of this series, we'll make a second attempt at generalizing this algorithm!
Appendix
{-# LANGUAGE MultiParamTypeClasses #-}
{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE ScopedTypeVariables #-}
module Dijkstra2 where
import Data.Hashable (Hashable)
import qualified Data.Heap as H
import Data.Heap (MinPrioHeap)
import qualified Data.HashSet as HS
import Data.HashSet (HashSet)
import Data.HashMap.Strict (HashMap)
import qualified Data.HashMap.Strict as HM
import Data.Maybe (fromMaybe)
data Distance a = Dist a | Infinity
deriving (Show, Eq)
instance (Ord a) => Ord (Distance a) where
Infinity <= Infinity = True
Infinity <= Dist x = False
Dist x <= Infinity = True
Dist x <= Dist y = x <= y
addDist :: (Num a) => Distance a -> Distance a -> Distance a
addDist (Dist x) (Dist y) = Dist (x + y)
addDist _ _ = Infinity
(!??) :: (Hashable k, Eq k) => HashMap k (Distance d) -> k -> Distance d
(!??) distanceMap key = fromMaybe Infinity (HM.lookup key distanceMap)
newtype Graph node cost = Graph
{ edges :: HashMap node [(node, cost)] }
class DijkstraGraph graph node cost where
dijkstraEdges :: graph -> node -> [(node, cost)]
instance DijkstraGraph (Graph String Int) String Int where
dijkstraEdges g n = fromMaybe [] (HM.lookup n (edges g))
data DijkstraState node cost = DijkstraState
{ visitedSet :: HashSet node
, distanceMap :: HashMap node (Distance cost)
, nodeQueue :: MinPrioHeap (Distance cost) node
}
findShortestDistance :: forall graph node cost. (Hashable node, Eq node, Num cost, Ord cost, DijkstraGraph graph node cost) => graph -> node -> node -> Distance cost
findShortestDistance graph src dest = processQueue initialState !?? dest
where
initialVisited = HS.empty
initialDistances = HM.singleton src (Dist 0)
initialQueue = H.fromList [(Dist 0, src)]
initialState = DijkstraState initialVisited initialDistances initialQueue
processQueue :: DijkstraState node cost -> HashMap node (Distance cost)
processQueue ds@(DijkstraState v0 d0 q0) = case H.view q0 of
Nothing -> d0
Just ((minDist, node), q1) -> if node == dest then d0
else if HS.member node v0 then processQueue (ds {nodeQueue = q1})
else
-- Update the visited set
let v1 = HS.insert node v0
-- Get all unvisited neighbors of our current node
allNeighbors = dijkstraEdges graph node
unvisitedNeighbors = filter (\(n, _) -> not (HS.member n v1)) allNeighbors
-- Fold each neighbor and recursively process the queue
in processQueue $ foldl (foldNeighbor node) (DijkstraState v1 d0 q1) unvisitedNeighbors
foldNeighbor current ds@(DijkstraState v1 d0 q1) (neighborNode, cost) =
let altDistance = addDist (d0 !?? current) (Dist cost)
in if altDistance < d0 !?? neighborNode
then DijkstraState v1 (HM.insert neighborNode altDistance d0) (H.insert (altDistance, neighborNode) q1)
else ds
graph1 :: Graph String Int
graph1 = Graph $ HM.fromList
[ ("A", [("D", 100), ("B", 1), ("C", 20)])
, ("B", [("D", 50)])
, ("C", [("D", 20)])
, ("D", [])
]Dijkstra's Algorithm in Haskell
In some of my recent streaming sessions (some of which you can see on my YouTube chanel), I spent some time playing around with Dijkstra’s algorithm. I wrote my own version of it in Haskell, tried to generalize it to work in different settings, and then used it in some examples. So for the next couple weeks I’ll be writing about those results. Today I’ll start though with a quick overview of a basic Haskell approach to the problem.
Note: This article will follow the “In Depth” reading style I talked about last week. I’ll be including all the details of my code, so if you want to follow along with this article, everything should compile and work! I’ll list dependencies, imports, and the complete code in an appendix at the end.
Pseudocode
Before we can understand how to write this algorithm in Haskell specifically, we need to take a quick look at the pseudo code. This is adapted from the Wikipedia description
function Dijkstra(Graph, source):
for each vertex v in Graph.Vertices:
dist[v] <- INFINITY
add v to Q
dist[source] <- 0
while Q is not empty:
u <- vertex in Q with min dist[u]
remove u from Q
for each neighbor v of u still in Q:
alt <- dist[u] + Graph.Edges(u, v)
if alt < dist[v] and dist[u] is not INFINITY:
dist[v] <- alt
return dist[]There are a few noteworthy items here. This code references two main structures. We have dist, the mapping of nodes to distances. There is also Q, which has a special operation “vertex in Q with min dist[u]”. It also has the operation “still in Q”. We can actually separate this into two items. We can have one structure to track the minimum distance to nodes, and then we have a second to track which ones are “visited”.
With this in mind, we can break the "Dijkstra Process" into 5 distinct steps.
- Define our type signature
- Initialize a structure with the different items (
Q,dist, etc.) in their initial states - Write a loop for processing each element from the queue.
- Write an inner loop for processing each “neighbor” we encounter of the items pulled from the queue.
- Get our answer from the final structure.
These steps will help us organize our code. Before we dive into the algorithm itself though, we’ll want a few helpers!
Helpers
There are a few specific items that aren’t really part of the algorithm, but they’ll make things a lot smoother for us. First, we’re going to define a new “Distance” type. This will include a general numeric type for the distance but also include an “Infinity” constructor, which will help us represent the idea of an unreachable value.
data Distance a = Dist a | Infinity
deriving (Show, Eq)We want to ensure this type has a reasonable ordering, and that we can add values with it in a sensible way. If we rely on a simple integer type maxBound, we’ll end up with arithmetic overflow problems.
instance (Ord a) => Ord (Distance a) where
Infinity <= Infinity = True
Infinity <= Dist x = False
Dist x <= Infinity = True
Dist x <= Dist y = x <= y
addDist :: (Num a) => Distance a -> Distance a -> Distance a
addDist (Dist x) (Dist y) = Dist (x + y)
addDist _ _ = InfinityNow we’ll be tracking our distances with a Hash Map. So as an extra convenience, we’ll add an operator that will look up a particular item in our map, returning its distance if that exists, but otherwise returning “Infinity” if it does not.
(!??) :: (Hashable k, Eq k) => HashMap k (Distance d) -> k -> Distance d
(!??) distanceMap key = fromMaybe Infinity (HM.lookup key distanceMap)Type Signature
Now we move on to the next step in our process: defining a type signature. To start, we need to ask, "what kind of graph are we working with?" We’ll generalize this in the future, but for now let’s assume we are defining our graph entirely as a map of “Nodes” (represented by string names) to “Edges”, which are tuples of names and costs for the distance.
newtype Graph = Graph
{ edges :: HashMap String [(String, Int)] }Our dijkstra function will take such a graph, a starting point (the source), and an ending point (the destination) as its parameters. It will return the “Distance” from the start to the end (which could be infinite). For now, we’ll exclude returning the full path, but we’ll get to that by the end of the series.
findShortestDistance :: Graph -> String -> String -> Distance IntWith our graph defined more clearly now, we’ll want to define one more “stateful” type to use within our algorithm. From reading the pseudo code, we want this to contain three structures that vary with each iteration.
- A set of nodes we’ve visited.
- The distance map, from nodes to their “current” distance values
- A queue allowing us to find the “unvisited node with the smallest current distance”.
For the first two items, it's straightforward to see what types we use. A HashSet of strings will suffice for the visited set, and likewise a HashMap will help us track distances. For the queue, we need to be a little clever, but a priority heap using the distance and the node will be most helpful.
data DijkstraState = DijkstraState
{ visitedSet :: HashSet String
, distanceMap :: HashMap String (Distance Int)
, nodeQueue :: MinPrioHeap (Distance Int) String
}Initializing Values
Now for step 2, let’s build our initial state, taking the form of the DijkstraState type we defined above. Initially, we will consider that there are no visited nodes. Then we’ll define that the only distance we have is a distance of “0” to the source node. We’ll also want to store this pair in the queue, so that the source is the first node we pull out of our queue.
findShortestDistance :: Graph -> String -> String -> Distance Int
findShortestDistance graph src dest = ...
where
initialVisited = HS.empty
initialDistances = HM.singleton src (Dist 0)
initialQueue = H.fromList [(Dist 0, src)]
initialState = DijkstraState initialVisited initialDistances initialQueue
...Processing the Queue
Now we’ll write a looping function that will process the elements in our queue. This function will return for us the mapping of nodes to distances. It will take the current DijkstraState as its input. Remember that the most basic method we have of looping in Haskell, particularly when it comes to a “while” loop, is a recursive function.
Every recursive function needs at least one base case. So let’s start with one of those. If the queue is empty, we can return the map as it is.
findShortestDistance graph src dest = ...
where
...
processQueue :: DijkstraState -> HashMap String (Distance Int)
processQueue ds@(DijkstraState v0 d0 q0) = case H.view q0 of
Nothing -> d0
...Next there are cases of the queue containing at least one element. Suppose this element is our destination. We can also return the distance map immediately here, as it will already contain the distance to that point.
findShortestDistance graph src dest = ...
where
...
processQueue :: DijkstraState -> HashMap String (Distance Int)
processQueue ds@(DijkstraState v0 d0 q0) = case H.view q0 of
Nothing -> d0
Just ((minDist, node), q1) -> if node == dest then d0
else ...One last base case: if the node is already visited, then we can immediately recurse, except plugging in the new queue q1 for the old queue.
findShortestDistance graph src dest = ...
where
...
processQueue :: DijkstraState -> HashMap String (Distance Int)
processQueue ds@(DijkstraState v0 d0 q0) = case H.view q0 of
Nothing -> d0
Just ((minDist, node), q1) -> if node == dest then d0
else if HS.member node v0 then processQueue (ds {nodeQueue = q1})
else ...Now, on to the recursive case. In this case we will do 3 things.
- Pull a new node from our heap and consider that node “visited”
- Get all the “neighbors” of this node
- Process each neighbor and update its distance
Most of the work in step 3 will happen in our “inner loop”. The basics for the first two steps are quite easy.
findShortestDistance graph src dest = ...
where
...
processQueue :: DijkstraState -> HashMap String (Distance Int)
processQueue ds@(DijkstraState v0 d0 q0) = case H.view q0 of
Nothing -> d0
Just ((minDist, node), q1) -> if node == dest then d0
else if HS.member node v0 then processQueue (ds {nodeQueue = q1})
else
-- Update the visited set
let v1 = HS.insert node v0
-- Get all unvisited neighbors of our current node
allNeighbors = fromMaybe [] (HM.lookup node (edges graph))
unvisitedNeighbors = filter (\(n, _) -> not (HS.member n v1)) allNeighborsNow we just need to process each neighbor. We can do this using a fold. Our “folding function” will have a type signature that incorporates the current node as a “fixed” argument while otherwise following the a -> b -> a pattern of a left fold. Each step will incorporate a new node with its cost and update the DijkstraState. This means the a value in our folding function is DijkstraState, while the b value is (String, Int).
foldNeighbor :: String -> DijkstraState -> (String, Int) -> DijkstraStateWith this type signature set, we can now complete our processQueue function before implementing this inner loop. We call a foldl over the new neighbors, and then we recurse over the resulting DijkstraState.
findShortestDistance graph src dest = ...
where
...
processQueue :: DijkstraState -> HashMap String (Distance Int)
processQueue ds@(DijkstraState v0 d0 q0) = case H.view q0 of
...
else
-- Update the visited set
let v1 = HS.insert coord v0
-- Get all unvisited neighbors of our current node
allNeighbors = fromMaybe [] (HM.lookup node (edges graph))
unvisitedNeighbors = filter (\(n, _) -> not (HS.member n v1)) allNeighbors
-- Fold each neighbor and recursively process the queue
in processQueue $ foldl (foldNeighbor node) (DijkstraState v1 d0 q1) unvisitedNeighborsThe Final Fold
Now let’s write this final fold, our “inner loop” function foldNeighbor. The core job of this function is to calculate the “alternative” distance to the given neighbor by going “through” the current node. This consists of taking the distance from the source to the current node (which is stored in the distance map) and adding it to the specific edge cost from the current to this new node.
foldNeighbor :: String -> DijkstraState -> (String, Int) -> DijkstraState
foldNeighbor current (DijkstraState v1 d0 q1) (neighborNode, cost) =
let altDistance = addDist (d0 !?? current) (Dist cost)
...We can then compare this distance to the existing distance we have to the neighbor in our distance map (or Infinity if it doesn’t exist, remember).
foldNeighbor current ds@(DijkstraState _ d0 _) (neighborNode, cost) =
let altDistance = addDist (d0 !?? current) (Dist cost)
in if altDistance < d0 !?? neighborNode
...If the alternative distance is smaller, we update the distance map by associating the neighbor node with the alternative distance and return the new DijkstraState. We also insert the new distance into our queue. If the alternative distance is not better, we make no changes, and return the original state.
foldNeighbor current ds@(DijkstraState _ d0 _) (neighborNode, cost) =
let altDistance = addDist (d0 !?? current) (Dist cost)
in if altDistance < d0 !?? neighborNode
then DijkstraState v1 (HM.insert neighborNode altDistance d0) (H.insert (altDistance, neighborNode) q1)
else dsNow we are essentially done! All that’s left to do is run the process queue function from the top level and get the distance for the destination point.
findShortestDistance :: Graph -> String -> String -> Distance Int
findShortestDistance graph src dest = processQueue initialState !?? dest
where
initialState = ...
processQueue = ...Our code is complete, and we can construct a simple example and see that it works!
graph1 :: Graph
graph1 = Graph $ HM.fromList
[ ("A", [("D", 100), ("B", 1), ("C", 20)])
, ("B", [("D", 50)])
, ("C", [("D", 20)])
, ("D", [])
]
...
{- GHCI -}
>> findShortestDistance graph1 “A” “D”
40Next Steps
This algorithm is nice, but it’s very limited and specific to how we’ve constructed the Graph type. What if we wanted to expose a more general API to users?
Read on to see how to do this in the next part of this series!
Appendix
Here is the complete code for this article, including imports!
module DijkstraSimple where
{- required packages:
containers, unordered-containers, hashable
-}
import qualified Data.HashMap.Strict as HM
import Data.HashMap.Strict (HashMap)
import qualified Data.Heap as H
import Data.Heap (MinPrioHeap)
import qualified Data.HashSet as HS
import Data.HashSet (HashSet)
import Data.Hashable (Hashable)
import Data.Maybe (fromMaybe)
data Distance a = Dist a | Infinity
deriving (Show, Eq)
instance (Ord a) => Ord (Distance a) where
Infinity <= Infinity = True
Infinity <= Dist x = False
Dist x <= Infinity = True
Dist x <= Dist y = x <= y
addDist :: (Num a) => Distance a -> Distance a -> Distance a
addDist (Dist x) (Dist y) = Dist (x + y)
addDist _ _ = Infinity
(!??) :: (Hashable k, Eq k) => HashMap k (Distance d) -> k -> Distance d
(!??) distanceMap key = fromMaybe Infinity (HM.lookup key distanceMap)
newtype Graph = Graph
{ edges :: HashMap String [(String, Int)] }
data DijkstraState = DijkstraState
{ visitedSet :: HashSet String
, distanceMap :: HashMap String (Distance Int)
, nodeQueue :: MinPrioHeap (Distance Int) String
}
findShortestDistance :: Graph -> String -> String -> Distance Int
findShortestDistance graph src dest = processQueue initialState !?? dest
where
initialVisited = HS.empty
initialDistances = HM.singleton src (Dist 0)
initialQueue = H.fromList [(Dist 0, src)]
initialState = DijkstraState initialVisited initialDistances initialQueue
processQueue :: DijkstraState -> HashMap String (Distance Int)
processQueue ds@(DijkstraState v0 d0 q0) = case H.view q0 of
Nothing -> d0
Just ((minDist, node), q1) -> if node == dest then d0
else if HS.member node v0 then processQueue (ds {nodeQueue = q1})
else
-- Update the visited set
let v1 = HS.insert node v0
-- Get all unvisited neighbors of our current node
allNeighbors = fromMaybe [] (HM.lookup node (edges graph))
unvisitedNeighbors = filter (\(n, _) -> not (HS.member n v1)) allNeighbors
-- Fold each neighbor and recursively process the queue
in processQueue $ foldl (foldNeighbor node) (DijkstraState v1 d0 q1) unvisitedNeighbors
foldNeighbor current ds@(DijkstraState v1 d0 q1) (neighborNode, cost) =
let altDistance = addDist (d0 !?? current) (Dist cost)
in if altDistance < d0 !?? neighborNode
then DijkstraState v1 (HM.insert neighborNode altDistance d0) (H.insert (altDistance, neighborNode) q1)
else ds
graph1 :: Graph
graph1 = Graph $ HM.fromList
[ ("A", [("D", 100), ("B", 1), ("C", 20)])
, ("B", [("D", 50)])
, ("C", [("D", 20)])
, ("D", [])
]Reading Style Results!
Earlier this week I proposed a poll, asking you what your preferred “Reading Style” is for Haskell articles. The results were fairly evenly split, although one answer did stand out a bit. Here are the results:
- In Depth Reading: 32%
- Quick Reference Guide: 23.8%
- General Haskell: 23.8%
- Code Ideas: 20.5%
The winner was In Depth Reading, which is really good for me to know! When I read personally, I tend not to have the patience to follow an entire article and copy the code from it. But apparently you, my readers, do enjoy it!
In a sense, this is good because I’ve often written with this style in mind. I tend to dislike tutorials that assume too much about the reader’s knowledge and what other tools they might be using. So I often try to make sure I include everything that might be important.
Going forward, I’ll try to have a good balance of article types, but with a slight emphasis on in depth tutorials. I’ll be tagging articles with their different types so you know what to expect when you’re reading it.
This will start next week, as I start writing about my work exploring Dijkstra’s algorithm. So check back in on Monday!
What's Your Reading Style?
I’ve been writing about Haskell for almost six years now. I’ve gone through a few different writing styles during that time, but I’m curious which of these most suit you, my readers! So for the first time, I’d like to take a poll and see what you think!
Here are four styles I could think of for how I would read an online programming article. Pick one of these to vote in this poll! (I’ll explain each option more below if you find these confusing).
If you have a style I haven’t thought of, you can email me (james@mondaymorninghaskell.me) and let me know! Here are the explanations in case you’re not sure.
In-Depth Reading
This is when you’re following the code I’m writing line-by-line, and you’ve got your editor open trying it out for yourself. You’re probably copying 10 or more lines of code from the article into your editor to see how it works.
Quick Reference Guide
This describes when you have a particular problem you’re trying to solve, like “what’s the best way to sort a list in Haskell?” or “How do I do a for-loop in Haskell?”. You want to find a code solution in the article so you can incorporate that code into your own project, but you don’t want to have to copy more than 4-5 lines of code.
This style also applies if you’re looking for a step-by-step guide to doing something with Haskell that isn’t specifically a code issue like, “How do I deploy a Haskell application on Heroku?”.
Learning Code Ideas
This means you’re interested in what Haskell code looks like, but you don’t specifically intend to copy any code from the article into your own work.
General Haskell Reader
This is you if you’re more interested in what Haskell is used for, and what distinguishes it from other languages. You want to read about these topics at the conceptual level without wading through a lot of code examples.
Vote!
I’ve probably done all of these approaches at some point. I’ve written many “project-oriented” series with an “In Depth” style in mind, especially around web skills and machine learning. Most of my work this year has been more along the lines of a “Quick Reference Guide”. The other two styles are less common, so if that’s what people are looking for I’d be very interested to hear about that! So let me know what you think! Cast your vote, and I’ll go through the results next week!
I'm Streaming on Twitch!
We’re done with our Data Structures series now, but before I get started with new material, I’d like to remind you that I do live coding most days of the week on Twitch! My streaming schedule usually looks something like this (all times are US Pacific time):
Monday: 30 minute stream (mid-day)
Tuesday: 30 minute stream (morning)
Wednesday: 30 minute stream (morning)
Thursday: 60 minute stream (evening)
Saturday: 60 minute stream (mid-day)
My exact timing varies a lot so you can follow me on Twitter as well to know when I’m going live! I try to give a 30-minute heads up before I start.
Starting in a couple weeks I’ll be writing about some of the work I’ve been doing on stream related to Dijkstra’s Algorithm in Haskell. I’ve published a few of the streaming sessions where I was working on this problem, so you can take a look at those past sessions now on my YouTube channel if you want to get a head start on this topic!
My next stream is tonight at 7:30 US Pacific time (GMT-07). I’ll be trying to make more IDEs and code editors work with Haskell, so be sure to check that out!
Data Structures: In Depth eBook!
Last week, we highlighted our new eBooks page with our At a Glance eBook. This week, as promised, we're releasing our new Data Structures: In Depth eBook.
This new eBook takes a deeper look at the topics and functions covered in our Data Structures series. You'll learn how Haskell's principle of immutability affects the design of its data structures, and see many more code examples for each function.
Best of all, this eBook gives you the chance to practice your skills with two problems for each data structure. The first problem will force you to come up with your own solution using the structure, and the second will let you see the performance characteristics of the structure by improving an existing solution to a problem.
After reading through the the 67 pages of this book and finishing the 18 problems, you'll be ready to use the right structure to solve any problem that comes your way in Haskell! So don't miss out! Find it on our eBooks page today!
Data Structures: At a Glance!
To cap off the Data Structures Series, we have a couple more resources to help you. The first of these is available right now, and you can check it out on our newly added eBooks page.
This first resouce is the "Data Structures At a Glance" eBook. It will allow you to get a super quick overview of all nine of the data structures in the series. All the type signatures of the most important functions for each structure are compressed on a sinigle page, so this can serve as an effective reference guide as you're trying to learn the structures.
The eBook is available on our eBooks page. It is free to download but uses "Pay What You Want" pricing so you can contribute to Monday Morning Haskell if you've really enjoyed our material!
Next Monday, we'll be coming out with our second Data Structure resource, so stay tuned for that!
Data Structures: Heaps!
Today we finish our Data Structures series! We have one more structure to look at, and that is the Heap! This structure often gets overlooked when people think of data structures, since its role is a bit narrow and specific. You can look at the full rundown on the series page here. If you've missed any of our previous structure summaries, here's the list:
That's all for our Data Structures series! The blog will be back soon with more content!
Data Structures: Sequences!
Haskell's basic "list" type works like a singly linked list. However, the lack of access to elements at the back means it isn't useful for a lot of algorithms. A double ended linked list (AKA a queue) allows a lot more flexibility.
In Haskell, we can get this double-ended behavior with the Sequence type. This type works like lists in some ways, but it has a lot of unique operators and mechanics. So it's worth reading up on it here in the latest part of our Data Structures Series. Here's a quick review of the series so far:
We have one more structure to look at next time, so this series is going to bleed into August a bit, so make sure to come back next week!
Data Structures: Vectors!
Last week we started looking at less common Haskell data structures, starting with Arrays. Today we're taking one step further and looking at Vectors. These combine some of the performance mechanics of arrays with the API of lists. Many operations are quite a bit faster than you can find with lists.
For a full review, here's a list of the structures we've covered so far:
We've got two more structures coming up, so stay tuned!
Data Structures: Arrays!
Throughout July we've been exploring different data structures in Haskell. I started out with a general process called 10 Steps for understanding Data Structures in Haskell. And I've now applied that process to five structures in Haskell:
Today we're going to start exploring some lesser-known structures in Haskell. Today's new structure is Arrays. While these are commonplace in other languages, you don't see them as often in Haskell, and Haskell's array behavior is a bit different from what you'll see elsewhere. So head over to the article page to read about it!